L’art fractal regorge de mystères et cache une infinité d’univers où se rencontrent préoccupations esthétiques et théories mathématiques. Mais que se cache-t-il vraiment derrière cette énième déclinaison des arts numériques ?

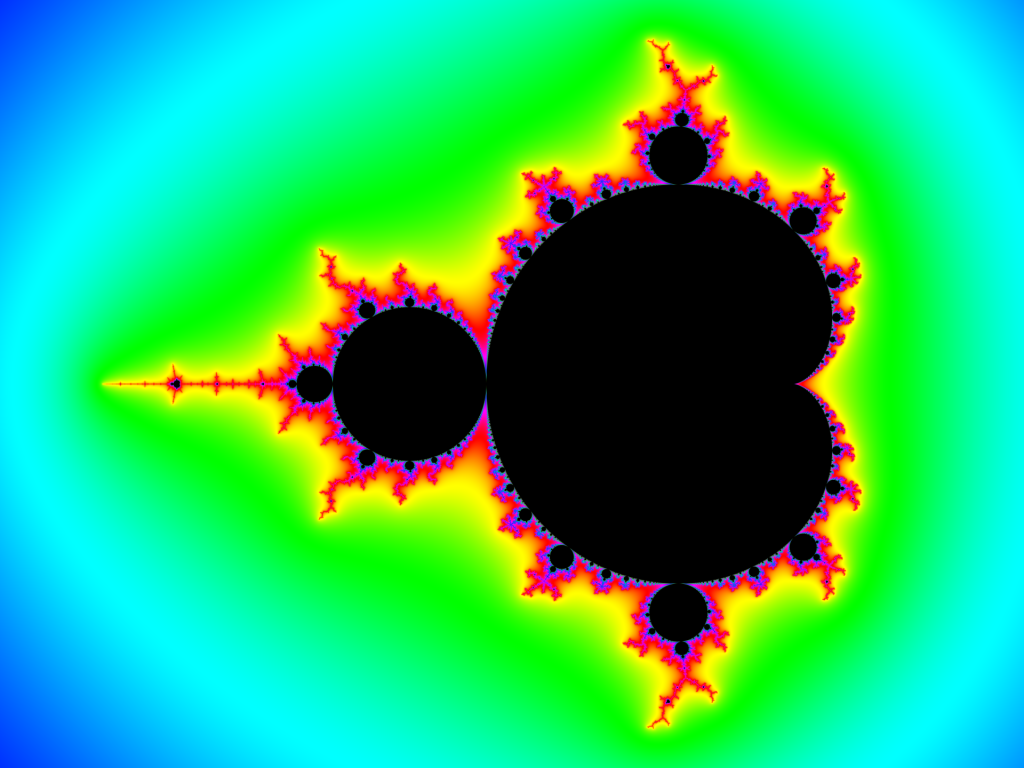



Il est vrai que la présence de mathématiques peut impressionner de prime abord. Si vous êtes, comme beaucoup, réfractaire à cette matière, que le simple fait d’en parler vous procure de l’urticaire, le réflexe logique serait de rester insensible à cette proposition esthétique. Si vous êtes aventureux, en revanche, c’est là la garanti de plonger dans un dédale infini, de découvrir un système de schémas répétés en boucle, une forme de poupée russe dont le motif principal est reproduit inlassablement, peu importe l’endroit où l’on zoome sur l’œuvre. Rattaché aux arts numériques, l’art fractal est effectivement constitué de formules mathématiques, obscures, parfois complexes, de celles que l’on rentre sur ordinateur afin de produire des formes pouvant être modulées et modifiées.
À titre d’exemple, Stephen Lotus, qui se décrit comme un « Voyageur Céleste », crée des images cosmiques colorées grâce à des applications mobiles : « Toutes mes œuvres sont réalisées sur mon téléphone, grâce auquel je peux utiliser la version mobile de Lightroom et de Photoshop, décrypte l’artiste, basé à Atlanta. La moitié de l’espace de stockage est occupée par plusieurs éditions de la même œuvre inachevée dans un millier de variantes de couleurs différentes. Les textures et les motifs de l’œuvre d’art ne sont qu’une fraction de l’expérience. Ce sont les couleurs et l’éclairage qui font toute la différence. Il faut donc que je réussisse ou que je ne réussisse pas ! » On comprend alors pourquoi Stephen Lotus peut passer parfois plusieurs mois sur une de ses créations avant d’être pleinement satisfait du résultat.
La légende de Mandelbrot
Pour comprendre toute la beauté et la subtilité de l’art fractal, il faut toutefois remonter à la source, poser un regard sur le travail de celui que l’on dit à l’origine de ce courant artistique : Benoît Mandelbrot. Le « père des fractales », comme il est nommé parfois, s’intéressait en premier lieu aux sciences pratiques. Mathématicien de formation, le Franco-Américain profite de ses recherches pour poser un regard curieux sur « l’art de rugosité », découvre peu à peu les fractales et développe une réflexion autours d’objets mathématiques appelés « ensembles de Julia ». C’est là, dans le cadre de ces études, que Benoît Mandelbrot en vient à transformer toutes ces données en images à l’aide d’un ordinateur : l’art fractal est né, et trouve sa définition autour d’une formule baptisée en son hommage, l’ensemble de Mandelbrot. Soit un ensemble de nombres complexes capable de produire des images aux frontières détaillées et aux éléments récursifs, tantôt rétrécis à l’infini, tantôt grossis.
« C’est grâce à Benoît Mandelbrot qu’environ la moitié de mon travail artistique existe »
Avec le temps, Benoît Mandelbrot est parvenu à démontrer comment, à partir de règles mathématiques simples, pouvait naître la complexité visuelle, comment le chaos graphique comporte finalement une part d’ordre, de règles à respecter. Inévitablement, un tel parti-pris ne pouvait qu’inspirer d’autres artistes, issus des générations suivantes. « C’est grâce à Benoît Mandelbrot qu’environ la moitié de mon travail artistique existe, affirme Stephen Lotus, reconnaissant. Bien que je n’utilise pas l' »ensemble de Mandelbrot » dans mon travail, les motifs que j’utilise ne seraient pas possibles sans lui ». En résumé : Benoît Mandelbrot est et reste la référence de l’art fractal, un courant qui, depuis les années 1980, a pourtant évolué et favorisé l’émergence de nouvelles possibilités graphiques.
L’immersion dans le monde fractal
Si les fractales connaissent une première belle exposition dans les années 1980, les évolutions technologiques permettent à ce concept de se développer et de gagner en précision au cours des décennies suivantes. Parce que de nombreux artistes commencent à s’y intéresser, parce que les progrès numériques se font sentir, et parce que les ordinateurs voient leur capacité de calcul s’améliorer. De fait, les recherches vont plus loin, et actent la transformation des fractales en art à part entière.
« Mon travail artistique consiste à capturer un instantané au milieu de quelque chose de comiquement épique »
À l’aube du 21ème siècle, une technique se démocratise et annonce une révolution visuelle : la 3D. Dès lors, il n’est plus question de créer uniquement des œuvres visuelles. Place aux mondes immersifs ! Des artistes tels que Stephen Lotus et Julius Horsthuit le savent pertinemment, et se plongent volontiers dans les formules mathématiques afin de créer des univers à part entière. Que ce voit via l’image ou la vidéo, la puissance infinie des fractales permet aux artistes d’explorer une myriade de possibilités. Stephen Lotus, par exemple, est allé jusqu’à se constituer sa propre marque de fabrique : « Mon travail artistique consiste à capturer un instantané au milieu de quelque chose de comiquement épique, confie-t-il. Il s’agit de phénomène cosmique que j’observe en traversant le vaste inconnu galactique. Pour ce faire, je me concentre sur un type ou une texture. Il y a le mouvement pour les thèmes de la nébuleuse en fusion ; le mouvement à 360 degrés vers l’extérieur pour les thèmes des étoiles et de l’hyperespace. Je combine l’un de ces styles avec un motif fractal afin de créer quelque chose d’encore plus épique ».
La révolution Mandelbulb
En 2009, une autre révolution s’annonce et se concrétise sous la forme de la première fractale 3D : le Mandelbulb, nommé ainsi en hommage à l’indispensable Benoît Mandelbrot. Cette grande (et nécessaire) évolution est à mettre au compte de Daniel White et Paul Nylander, dont le travail s’appuie sur l’aide de plusieurs utilisateurs des Fractals Forums – preuve, s’il en fallait encore une, que les arts numériques sont foncièrement collaboratifs.
Concrètement, un Mandelbulb n’est rien d’autre qu’une représentation en 3D d’un ensemble de Mandelbrot. De là à considérer cette évolution comme une simple mutation ? Non, il s’agit plutôt là d’un lent et méticuleux processus étiré sur deux années de tests et d’équations mathématiques. un travail colossal, donc, qui a au moins deux mérites : 1/avoir ouvert la voie aux artistes et à l’art fractal tel qu’il se conçoit à l’heure actuelle ; 2/nous renvoyer aux mots d’Euripide qui, il y a plus de 2000 ans, résumait sans le savoir ce que pourrait être l’art fractal : « Puissant est la géométrie ; joint à l’art, sans résistance ».